Mario
ha deciso di provare a sostituire la molla di carica
di un suo orologio e mi ha chiesto di parlare di questo importante
componente .
La molla di carica è , nella quasi totalità dei
casi, un lungo nastro d'acciaio , o di altro
materiale, che fornisce all'orologio l'energia necessaria per
funzionare.
Le sue dimensioni, spessore e altezza vengono
stabilite in funzione dell'energia che la molla dovrà
fornire al sistema e, per quanto concerne la lunghezza,
in base alla durata di carica che si vuole ottenere.
Detto nastro viene avvolto su un asse in un cilindro di metallo
che viene chiamato bariletto.
Il bariletto viene dimensionato in base alle dimensioni della
molla di carica ed è quindi molto importante che, presentatasi
per una qualunque ragione, la necessità di doverla sostituire,
la lunghezza della molla stessa sia quella corretta
in relazione al diametro esterno dell'albero ed a quello interno
del bariletto, e ciò perché
sia disponibile il maggior numero possibile di giri del bariletto.
Una
molla più corta o una più lunga di quella di una
lunghezza corretta genereranno entrambe un minore numero di
giri.( riducendo così, ovviamente, il periodo di durata
della carica dell'orologio).
Possiamo
così stabilire il valore di Rm che è
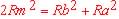
Ovvero
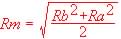
Siamo
franchi! Possiamo sbilanciarci ed affermare che quasi certamente,
piuttosto che calcolare il valore esatto delle dimensioni della
molla da utilizzare in un determinato bariletto, i più,
si fideranno di un proprio giudizio approssimativo
basato per taluni sulla loro esperienza e per altri dettato
dalla loro inesperienza.
L'universo
degli orologiai è fatto di persone eclettiche che raramente
si fermano (...o forse è meglio dire , si fermavano !)
di fronte a delle difficoltà!
Suanier riporta nel suo " Trattato
sulla Moderna Orologeria" del 1861 un estratto
di uno scritto di un orologiaio, tale M.M. Roze,
in cui l'autore afferma di aver disegnato un calibro con
il quale potersi accertare della correttezza della lunghezza
di una molla collocata dentro ad un bariletto.
Il suo approccio teorico al problema è il seguente:
Sia P il punto che divide in 2 parti eguali,
x e y, il segmento Rb-Ra.
La perpendicolare all'asse verticale del bariletto passante
per P interseca il diametro interno della molla
scarica in Q.
Per A e B aventi la stessa
area , Monsiuer Roze dimostra che x
= y = z .
Orbene, essendo
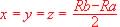
applicando il teorema di Pitagora al triangolo rettangolo OPQ
avremo che
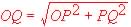
ovvero
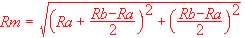
e semplificando

lo stesso risultato che avevamo ottenuto precedentemente.
Basandosi quindi sul fatto che Q è il vertice
di un quadrato la cui diagonale è Rb-Ra,
Monsieur Roze ha disegnato un calibro con il
quale è possibile stabilire immediatamente se la lunghezza
della molla di carica è appropriata per il bariletto
che la ospita.
Appoggiando
il punto A della parte inferiore del calibro
sull'albero del bariletto e facendo scorrere la parte superiore
del calibro stesso fino a quando il punto B
si sovrappone ad un punto della circonferenza interna del bariletto,
solo se un punto del diametro interno della molla scarica
coinciderà con C, la molla di carica avrà una
lunghezza corretta..
Costruire questo strumento , anche solo con del compensato ,
è un gioco da ragazzi , e Mario non avrà ora scusanti
se adopererà per il suo orologio una molla di carica
"sbagliata".....
Prossimamente
parliamo del compasso per orologiai