Gli orologiai del 18 secolo, ottimi artigiani, avevano in genere una scarsa conoscenza della teoria legata alla progettazione degli ingranaggi, che costruivano usando regole approssimative e ciascuno le proprie.

Questa è una ragione per cui quando si deve sostituire una ruota dentata di un vecchio orologio è difficile, se non pressoché impossibile, stabilire esattamente quale fresa a modulo usare e bisogna quindi cercare qualche compromesso.

Con il passare del tempo si è sentita la necessità di omogeneizzare i parametri che regolano la forma dei denti, delle ruote e dei pignoni, anche perché l'industria, per accelerare i tempi di produzione, richiedeva degli standard ben precisi.

Peraltro, le specifiche degli ingranaggi industriali, dovendo rispondere a esigenze diverse, sono differenti da quelli degli ingranaggi usati in orologeria: ed ovviamente è verso questi ultimi che rivolgiamo la nostra attenzione.

Immaginiamo due dischi di diverso diametro a contatto fra loro sulle loro circonferenze: se uno gira, ed esiste sufficiente attrito fra di essi, l'altro ruoterà a sua volta con un rapporto di giri proporzionale ai diametri dei due dischi.

Purtroppo , come si può facilmente immaginare, in pratica, una siffatto accoppiamento non offre garanzia di uniformità di trasmissione del movimento in quanto potrebbero verificarsi degli slittamenti .
Quindi onde evitare lo scorrimento fra le parti , sintetizzando, formiamo parte del dente al di sopra della circonferenza di ciascun disco, e parte al di sotto.

Abbiamo così introdotto 3 concetti importanti:

a) la circonferenza di riferimento per la costruzione della ruota dentata ovvero la circonferenza primitiva e quindi il suo diametro primitivo (dp).
b) la parte del dente al di sopra della circonferenza primitiva che viene chiamata addendum
c) la parte del dente al di sotto della circonferenza primitiva che viene chiamata dedendum.

La forma del dente, l'insieme dell'addendum e del dedendum, deve rispondere agli standard contenuti nelle norme svizzere N.H.S. 56702 e 56703 ed B.S. 978 parte 2 (... per chi ha voglia di andarsele a vedere...).
E così possiamo definire il modulo ( m ) di una ruota dentata il rapporto tra il diametro primitivo ed il numero dei denti ( Z ) tagliati, ovvero:

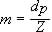
che si intende un numero puro, senza unità di misura.

Divagazione
Io non ci credo, ma forse gli Inglesi, ai quali tanto dobbiamo per quanto concerne "la tecnica", con l'introduzione dell'Euro saranno costretti ad uniformarsi ai nostri standard. Fino a ieri non lo hanno fatto.

"Noi", per definire il passo di una filettatura misuriamo l'avanzamento per filetto, "loro", quanti filetti si contano in un pollice. Quindi, mentre nel sistema metrico l'incremento del numero che rappresenta il passo significa "un filetto più grosso" , al contrario, in quello inglese , detto incremento indica un "filetto più piccolo".
Ed anche per quanto riguarda le ruote dentate non si smentiscono.

Il loro Diametral Pitch (DP) , il corrispondente del nostro m, indica il rapporto tra il numero dei denti ed il diametro primitivo della disco in cui vengono tagliati, ovvero:



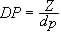
.... esattamente l'opposto di quello che abbiamo definito il modulo .... speriamo nell'Euro......

Conoscendo due dati , per esempio il modulo ed il numero dei denti, possiamo risalire al diametro primitivo, anche se questo, da un punto di vista pratico. è un dato poco significativo per la costruzione di una ruota , infatti quello di cui abbiamo bisogno è il diametro esterno.

Tagliamo la nostra prima ruota.