|
Tante
volte l'abbiamo ripetuto che oramai sappiamo che il periodo
di oscillazione di un pendolo è direttamente proporzionale
alla sua lunghezza . Più detta lunghezza aumenta, più
tempo il pendolo impiega per completare la sua oscillazione.
In certi campanili , dove lo spazio lo consente , vengono impiegati
per gli orologi dei pendoli anche da 2 secondi e più,
e quindi proporzionalmente lunghi.
Divagazione
Stabilire
se l'incremento di queste dimensioni migliori la qualità
del pendolo , ormai siamo in grado di stabilirlo( ....se non vi
siete dimenticati del fattore
di qualità "Q": ... è aumentata la
massa e quindi probabilmente sono aumentate le resistenze, la
frequenza è sicuramente diminuita.... e grazie a Dio, almeno
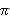 è
rimasto costante.....), ma non è di questo di cui vogliamo
parlare. è
rimasto costante.....), ma non è di questo di cui vogliamo
parlare.
Come
al solito il nostro cammino è disseminato di "se"
e "ma" ed una rigorosa applicazione del concetto sopra
espresso potrebbe portare alla errata conclusione che un
pendolo di lunghezza infinita abbia un periodo p
che aumenti il suo valore senza limiti.
|
Una
assunzione fra le tante che limita la validità
di
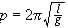
è che nel calcolo del periodo , il campo gravitazionale
in cui si muove il pendolo viene considerato parallelo
ed uniforme.
|
A onor del vero questa assunzione è più che accettabile
per un comune pendolo, ma noi sappiamo che le cose non stanno
così in quanto detto campo non è ne uniforme e tanto
meno parallelo , bensì diretto ( anche questa una assunzione)
verso il centro della terra .
Ora, se ad essere considerato è un pendolo la cui lunghezza
è molto grande, non possiamo non tener conto che l'assunzione
sul campo gravitazionale è errata.
Rawlings ( op. cit. ) ha calcolato il periodo
di un pendolo che si muove nel campo gravitazionale terrestre
ottenendo come risultato
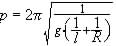
dove
l è la lunghezza del pendolo
R il raggio della terra.
| Con
l che tende all'infinito e con un paio di passaggi si
ottiene che p ha come valore limite
|
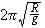 |
|
e facendo le adeguate sostituzioni, 84 minuti primi circa
|
Ritorniamo
con i piedi per terra e parliamo di
ingranaggi
|