Divagazione
Sto parlando con degli appassionati, ormai con degli esperti, e quindi, discutendo di cose pratiche, un linguaggio più immediato si impone. L'ultima frase avrebbe potuto essere " Immaginiamo un orologio provvisto di un pendolo la cui oscillazione ha un periodo di 2 minuti secondi e con la lancetta dei minuti secondi fissata sull'asse della ruota dello scappamento". Sono certo concorderete che tanta pignoleria, in questo caso, fra esperti, potrebbe non essere necessaria. :o)

Perché la lancetta dei secondi compia un giro e sia trascorso un minuto primo, il pendolo dovrà aver compiuto 60 alternanze e la ruota dello scappamento avere 30 denti ( 30 in quanto ciascun dente è impegnato per due volte dalle palette dell'ancora.).

Peraltro nel nostro orologio la ruota di centro ( quella fissata sull'asse che porta anche la lancetta dei minuti ) deve compiere un giro in 60 minuti.. Il nostro orologio dovrà quindi avere un treno di ingranaggi che adempia a queste due premesse.

Dato che il numero delle alternanze in un'ora deve essere , nel nostro caso, 60 alternanze/minuto per 60 minuti primi , ovvero 3600, dovremo prevedere che per ogni alternanza la ruota di centro avanzi di 1/3600.
Che è come dire che per ogni giro della ruota di centro, il pendolo dovrà compiere 3600 oscillazioni.

Noi dovremo quindi calcolare un treno di ingranaggi la cui riduzione soddisfi questa esigenza . Dovrà quindi essere che il numero dei denti della ruota di centro diviso il numero delle ali del pignone con il quale ingrana, moltiplicato il numero dei denti della seconda ruota diviso il numero delle ali del pignone con il quale ingrana , moltiplicato 2 volte il numero dei denti della ruota di scappamento sia eguale a 3600.

Divagazione
Che fine ha fatto la prima ruota? Abbiamo parlato di ruota di centro e di seconda ruota, ma nessun accenno alla prima. . Semplicemente non esiste! I maestri orologiai di un tempo hanno preferito questa terminologia : ruota di centro, poi seconda ruota ,eventualmente una terza, una quarta e poi ruota di scappamento.

Se indichiamo con Z il numero dei denti delle ruote dentate e con p quello delle ali dei pignoni possiamo generalizzare il concetto scrivendo:

Alternanze/ora =		ovvero =
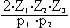e facilmente il numero delle alternanze al minuto primo si otterrà dividendo per 60 ( minuti) il risultatodell'equazione appena scritta, ovvero =

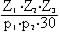
Calcoliamo il numero di alternanze al minuto primo per il treno di ingranaggi che propongo qua a fianco. Esso sarà eguale a (84 x 77 x 35)/(7 x 7 x 30) = 154 Dividendo questo numero per 60 ( minuti secondi, m") sapremo quante alternanze di compiono in un secondo, ovvero 154/60= 2.566... ....e per conoscere la durata di ogni alternanza basterà calcolare 1(uno) diviso 2.566.. ovvero 0.389... .... anche se ormai sfiniti sappiamo ora quando dura una alternanza del pendolo dell'orologio di cui stiamo parlando. Ed ora sono certo sarete voi a suggerirmi la formula per calcolare la lunghezza del pendolo. in funzione del suo periodo ed ascoltando quello che con sicurezza dettate, scrivo:

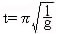e prendo atto del fatto che non esitate a sottolineare che questa è solo una formula

Finalmente possiamo scrivere

l =

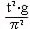ed assumendo

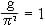(uno)

,l

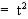
e nel nostro caso l = 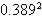ovvero = 151.32 mm.

Abbiamo dato soddisfazione a Harrison ,...John, non Ford... ed abbiamo calcolato la lunghezza teorica (approssimativa) del pendolo del nostro orologio , ... ma poi in pratica